
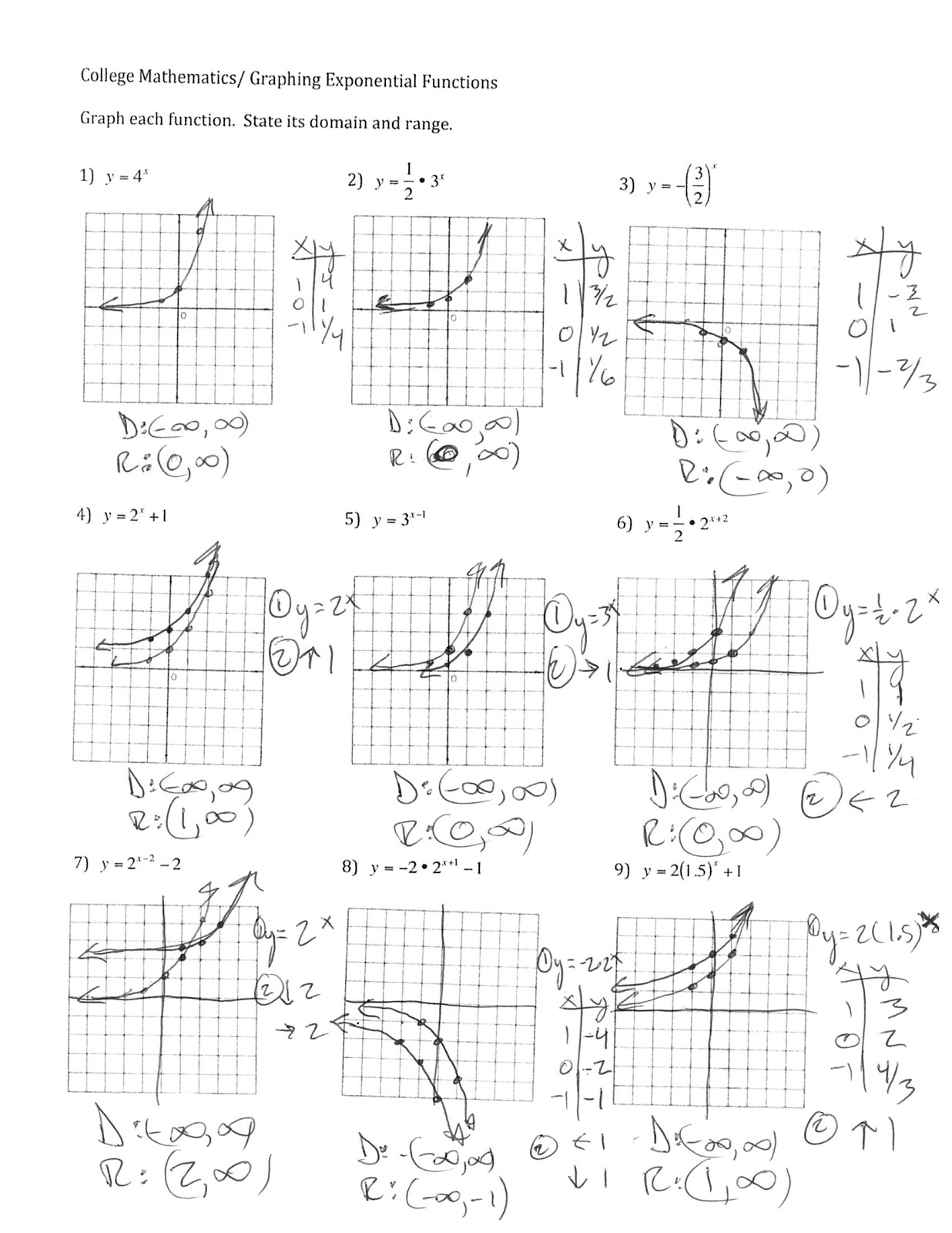
For example, if we look at exponential function whose base 2, nf(64) = 2 64 =18, 446, 744, 073, 709, 525, 000 f(64) = 2 64 =18, 446, 744, 073, 709, 525, 000 And 2 n t even f(64) a very= big 2 64 number =18, 446, to744, be 073, using709, for525, a base 000 (any positive number And 2 n t can be even a base, a very bigplenty number numbers to using are much, for a base much(any bigger positive than 2). does n For example, grow if webigger look at as it moves exponential to right, function butwhose it gets base big in2, a n hurry. doesfor example, grow if we bigger lookas atit moves exponential to right, function but whose it gets base big Not in aonly 2, hurry. Not only does grow bigger as it moves to right, but it gets bignot in a hurry. becomes becomes shorter shorter shorter, shorter, shrinking shrinking towards, towards, but but never never touching, touching, x-ax. The y-intercept at 1 when moving to right, grows 180Ĥ taller taller when moving to left, becomes shorter shorter, taller taller shrinking taller taller towards, when when moving moving but never to to touching, left, left, x-ax. f a greater than 1, n =a x grows taller as it moves to right. There are two options: eir base greater than 1, or base less than 1 (but still positive). * * * * * * * * * * * * * Graphs exponential functions t s really important you know general shape an exponential function. Forthreason,weusuallydon ttalkmuch about exponential function whose base equals 1. Base 1 f anexponentialfunctionwhosebaseequals1 if =1 x nforn, m 2 N we have n f =1 m p n m m = 1 n = mp 1=1 n fact, for any real number x, 1 x =1,s(x) =1 x same function as constant function =1. For example, 3 4 =81 a 0 =1 f n, m 2 N, n a n m = m p a n =( mp a) n a x = 1 a x The rules above were designed so following most important rule exponential functions holds: 178Ģ a x a y = a x+y Anor variant important rule above a x a y = ax y And re also following slightly related rule (a x ) y = a xy Examples = 2 p 4=7 0 =15 1 =15 (2 5 ) 2 =2 10 =1024 (3 20 ) 1 10 =3 2 = 1 (8) 2 3 = 1 ( 3p 8) 2 = 1 4 * * * * * * * * * * * * * 179ģ The base an exponential function f =a x, n we call a base exponential function. Rules for exponential functions Here are some algebra rules for exponential functions will be explained in class. The function =3 x an exponential function variable exponent. Here variable, x, being raed to some constant power.
There a big di erence between an exponential function a polynomial. For example, =3 x an exponential function, g(x) =( 4 17 )x an exponential function.
For any positive number a>0, re a function f : R! (0, 1) called an exponential function defined as =a x. When a quantity increases or decreases exponentially it increases or decreases by the same percent over equal time periods in comparison to when a compound increases or decreases linearly when a quantity increases or decreases with the same amount over equal time periods.1 Exponential Functions n th chapter, a will always be a positive number. In other words it is more profitable to have a compounded interest than a fixed return.Īn exponential function is a nonlinear function that has the form ofĪn exponential function with a > 0 and b > 1, like the one above, represents an exponential growth and the graph of an exponential growth function rises from left to right.Īn exponential function where a > 0 and 0 < b < 1 represents an exponential decay and the graph of an exponential decay function falls from left to right. The lower straight line represents the linear increase and the upper bowed curve represents the exponential increase. Now we shall examine the differences displayed with the functions in our example above in a coordinate system. The interest and thus also the function are exponentials.
Here we have an x-variable in the exponent. $$= initial\: capital \cdot compound\: interest^$$ $$investment \:\: after \: x \: number \: of\: years$$ However in the first case, the structure proceeds as: In this case we may note that the increase was constant each year. For example: If we have $50 000 deposited in the bank, and receive a 2 % interest annually, our investment shall increase as follows: YearĬompare that with what we would have with a linear increase (2%): Year

The function need not necessarily respond like a straight line equation. A straight line is known as a linear function. These types of equations are known as functions. All types of equations containing two unknown (x and y) variables may be inserted in a coordinate system. We have dealt with linear functions earlier.


 0 kommentar(er)
0 kommentar(er)
